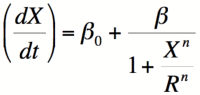Difference between revisions of "CellularMemory:Mathematical Models"
From GcatWiki
Wideloache (talk | contribs) |
Wideloache (talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | + | {DeLoache Top}} | |
=<center>Mathematical Models</center>= | =<center>Mathematical Models</center>= | ||
==The Hill Equation== | ==The Hill Equation== | ||
| − | + | * Three closely related mathematical models can be used to describe binding of two given molecules in a biological system. . All of them can be understood by looking at the definition of the dissociation constant of a given molecular complex. Kd = [A][B]/[AB]. Because [AB] = [Btotal] - [B] you can show that the percentage of unbound B molecules [B]/[Btotal] = 1/(1+X/Kd). If you think of B as a RNA Polymerase binding site and A as a repressor, multiply by the maximal rate of transcription (beta) yields the promoter activity as a function of repressor concentration. (See discussion of Kd below) | |
| + | * The value of K is closely related to the dissociation constant of the inducer/repressor complex. The dissociation constant measures the propensity for this complex to fall apart. Kd = [I][R]/[IR]. This gives the dissociation constant units of concentration. It can be shown mathematically that Kd is equal to [I] at which half of the repressor is bound to the DNA and half is not ([R] = [IR]). Because the amount of repressor bound to the DNA is proportional to the level of transcription, K (being closely related to Kd) is the value at the inducer yields half of the maximum level of transcription. | ||
| + | * Michaelis-Menton model doesn't take cooperativity into account. | ||
| + | * The Hill equation accounts for cooperativity of binding, but is not a completely accurate description at very low concentrations of repressor/activator. | ||
| + | *The Monod, Changeux, and Wymann model is the most accurate model of these three, but is not commonly used because of its increased complexity and the fact that the hill equation accurately describes most situations. | ||
| + | |||
[[Image: Hillactivator.png|thumb|200px|right|'''Equation 1:''' The Hill equation for an activator.]] | [[Image: Hillactivator.png|thumb|200px|right|'''Equation 1:''' The Hill equation for an activator.]] | ||
[[Image: Hillrepressor.png|thumb|200px|right|'''Equation 2:'''The Hill equation for a repressor.]] | [[Image: Hillrepressor.png|thumb|200px|right|'''Equation 2:'''The Hill equation for a repressor.]] | ||
| Line 11: | Line 16: | ||
==Cooperativity== | ==Cooperativity== | ||
| − | + | Show how Michaelis-Menton is the same as the hill equation when n=1 and then show what happens as n increases. (graph in book) | |
[[Image:Modelinggraphs.png|400px|right]] | [[Image:Modelinggraphs.png|400px|right]] | ||
[[Image:linebreak.png]] | [[Image:linebreak.png]] | ||
Revision as of 07:56, 29 November 2007
{DeLoache Top}}
Contents
Mathematical Models
The Hill Equation
- Three closely related mathematical models can be used to describe binding of two given molecules in a biological system. . All of them can be understood by looking at the definition of the dissociation constant of a given molecular complex. Kd = [A][B]/[AB]. Because [AB] = [Btotal] - [B] you can show that the percentage of unbound B molecules [B]/[Btotal] = 1/(1+X/Kd). If you think of B as a RNA Polymerase binding site and A as a repressor, multiply by the maximal rate of transcription (beta) yields the promoter activity as a function of repressor concentration. (See discussion of Kd below)
- The value of K is closely related to the dissociation constant of the inducer/repressor complex. The dissociation constant measures the propensity for this complex to fall apart. Kd = [I][R]/[IR]. This gives the dissociation constant units of concentration. It can be shown mathematically that Kd is equal to [I] at which half of the repressor is bound to the DNA and half is not ([R] = [IR]). Because the amount of repressor bound to the DNA is proportional to the level of transcription, K (being closely related to Kd) is the value at the inducer yields half of the maximum level of transcription.
- Michaelis-Menton model doesn't take cooperativity into account.
- The Hill equation accounts for cooperativity of binding, but is not a completely accurate description at very low concentrations of repressor/activator.
- The Monod, Changeux, and Wymann model is the most accurate model of these three, but is not commonly used because of its increased complexity and the fact that the hill equation accurately describes most situations.
Cooperativity
Show how Michaelis-Menton is the same as the hill equation when n=1 and then show what happens as n increases. (graph in book)
Determining the Values of Funcational Parameters
Put text here.
Quantitative Part Characterization
Put text here.
