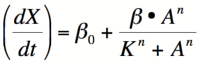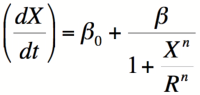Mathematical Models

Mathematical modeling is an important component in the construction of rationally designed gene networks. The complexity of biological systems makes necessary the use of sophisticated mathematical models to accurately predict network functionality. Models are useful in tuning the individual components of a network to increase system robustness. They also provide a basis for comparison of experimental results with expected results, allowing researchers to test the validity of their assumptions.

Modeling Transcription Rates

Note: the following mathematical analysis was developed based on a summary of the input function of a gene in An Introduction to Systems Biology: Design Principles of Biological Circuits (Alon, pgs. 241-250).

When dealing with gene activation and repression networks, such as those described in the common Biological Designs for synthetic cellular memory section of this paper, mathematical models are mainly used to model the transcription rate of a gene(s). Three common models that describe transcription rate as a function of complexity are, in order of increasing complexity, the Michaelis-Menten model, the Hill model, and the Monod-Wymann-Changeux model. Each of these model builds on the one preceding it to paint a clearer picture of how binding occurs between two or more molecules and how that binding affects transcription rates. The Hill equation is used most often to model cellular memory networks. It is described below in detail.

The Michaelis-Menten Equation

To describe how the Hill equation works, it is first helpful to examine the Michaelis-Menten equation. Based on the two biological designs presented in the previous section, it can be seen that to mathematically model these designs, we must be able to describe the effect of repressor/promoter binding on transcription rates (mutual repression) and the effect of activator/repressor binding on transcription rates (autoregulatory positive feedback). The Michaelis-Menten model allows us to do that using a simple equation.

Let's start by looking at the effect of repressor/promoter binding on transcription rate. The starting point for this proof is the dissociation constant for promoter and repressor binding. This constant, K_d, measures the tendency for a repressor/promoter complex to fall apart into its two separate subunits. The value is determined by the affinity of the two molecules for each other and is written as:

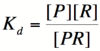
Here, [P] represents the concentration of unbound promoter, [R] represents the concentration of unbound repressor and [PR] represents the concentration of promoter/repressor complexes. Our goal from here is to derive an equation that gives the percentage of unbound promoters as a function of [R]. Because the percentage of unbound promoters is proportional to the rate of transcription, we can easily modify the equation to give us the transcription rate as a function of [R].

We can modify the equation above by substituting [P_tot] - [P] for [PR] because the concentration of unbound promoter plus the concentration of bound promoter equals the total promoter concentration.

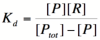
The Hill Equation

• Three closely related mathematical models can be used to describe binding of two given molecules in a biological system. . All of them can be understood by looking at the definition of the dissociation constant of a given molecular complex. Kd = [A][B]/[AB]. Because [AB] = [Btotal] - [B] you can show that the percentage of unbound B molecules [B]/[Btotal] = 1/(1+X/Kd). If you think of B as a RNA Polymerase binding site and A as a repressor, multiply by the maximal rate of transcription (beta) yields the promoter activity as a function of repressor concentration. (See discussion of Kd below)
• The value of K (the activation/repression coefficient) is closely related to the dissociation constant of the inducer/repressor complex. The dissociation constant measures the propensity for this complex to fall apart. Kd = [I][R]/[IR]. This gives the dissociation constant units of concentration. It can be shown mathematically that Kd is equal to [I] at which half of the repressor is bound to the DNA and half is not ([R] = [IR]). Because the amount of repressor bound to the DNA is proportional to the level of transcription, K (being closely related to Kd) is the value at the inducer yields half of the maximum level of transcription.
• Michaelis-Menton model doesn't take cooperativity into account.
• The Hill equation accounts for cooperativity of binding, but is not a completely accurate description at very low concentrations of repressor/activator.
• The Monod, Changeux, and Wymann model is the most accurate model of these three, but is not commonly used because of its increased complexity and the fact that the hill equation accurately describes most situations.

The Monod-Wymann-Changeux Equation

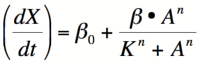Equation 1: The Hill equation for an activator.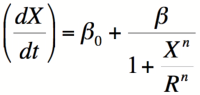

Equation 2:The Hill equation for a repressor.

Cooperativity

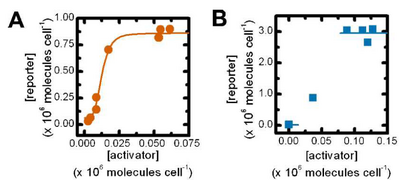
Show how Michaelis-Menton is the same as the hill equation when n=1 and then show what happens as n increases. (graph in book)

Determining the Values of Funcational Parameters

Put text here.

Quantitative Part Characterization

Put text here.