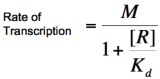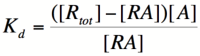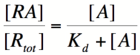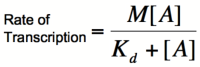Difference between revisions of "CellularMemory:Mathematical Models"
Wideloache (talk | contribs) |
Wideloache (talk | contribs) |
||
| Line 10: | Line 10: | ||
When dealing with gene activation and repression networks, such as those described in the common [[CellularMemory:Biological Designs |Biological Designs]] for synthetic cellular memory section of this paper, mathematical models are mainly used to model the transcription rate of a gene(s). Three common models that describe transcription rate as a function of repressor or activator are, in order of increasing complexity, the [http://en.wikipedia.org/wiki/Michaelis-Menten_kinetics Michaelis-Menten] model, the [http://en.wikipedia.org/wiki/Hill_equation Hill] model, and the [http://en.wikipedia.org/wiki/MWC_model Monod-Wymann-Changeux] model. Each of these model builds on the one preceding it to paint a clearer picture of how binding occurs between two or more molecules and how that binding affects transcription rates. | When dealing with gene activation and repression networks, such as those described in the common [[CellularMemory:Biological Designs |Biological Designs]] for synthetic cellular memory section of this paper, mathematical models are mainly used to model the transcription rate of a gene(s). Three common models that describe transcription rate as a function of repressor or activator are, in order of increasing complexity, the [http://en.wikipedia.org/wiki/Michaelis-Menten_kinetics Michaelis-Menten] model, the [http://en.wikipedia.org/wiki/Hill_equation Hill] model, and the [http://en.wikipedia.org/wiki/MWC_model Monod-Wymann-Changeux] model. Each of these model builds on the one preceding it to paint a clearer picture of how binding occurs between two or more molecules and how that binding affects transcription rates. | ||
| − | The Hill equation is used most often to model cellular memory networks. In order to describe how the Hill equation works, it is first helpful to examine a simpler model. Based on the two [[CellularMemory:Biological Designs |biological designs]] presented in the previous section, it can be | + | The Hill equation is used most often to model cellular memory networks. In order to describe how the Hill equation works, it is first helpful to examine a simpler model. Based on the two [[CellularMemory:Biological Designs |biological designs]] presented in the previous section, it can be reasoned that to mathematically model these designs, we must be able to describe the effect of repressor/promoter binding on transcription rates ([[CellularMemory:Biological Designs#Mutual Repression |mutual repression]]) and the effect of activator/repressor binding on transcription rates ([[CellularMemory:Biological Designs#Autoregulatory Positive Feedback |autoregulatory positive feedback]]). |
===Repressor/Promoter Binding=== | ===Repressor/Promoter Binding=== | ||
| Line 17: | Line 17: | ||
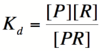
[[Image:PR1.png|100px]] | [[Image:PR1.png|100px]] | ||
| − | + | where [P] represents the concentration of unbound promoter, [R] represents the concentration of unbound repressor and [PR] represents the concentration of promoter/repressor complexes. Our goal from here is to derive an equation that gives the probability of unbound promoter as a function of [R]. Because the probability of unbound promoters is proportional to the rate of transcription, we can easily modify the equation to give us the transcription rate as a function of [R] by multiplying by the maximal rate of transcription. | |
We can modify the equation above by substituting [P<sub>total</sub>] - [P] for [PR] because the concentration of unbound promoter plus the concentration of bound promoter equals the total promoter concentration: | We can modify the equation above by substituting [P<sub>total</sub>] - [P] for [PR] because the concentration of unbound promoter plus the concentration of bound promoter equals the total promoter concentration: | ||
| Line 23: | Line 23: | ||
[[Image:PR2.png|120px]] | [[Image:PR2.png|120px]] | ||
| − | Using simple algebra, we can now solve for the | + | Using simple algebra, we can now solve for the probability of unbound promoter as a function of [R]: |
[[Image:PR3.png|140px]] | [[Image:PR3.png|140px]] | ||
| Line 34: | Line 34: | ||
===Activator/Repressor Binding (The Michaelis-Menten Equation)=== | ===Activator/Repressor Binding (The Michaelis-Menten Equation)=== | ||
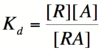
| + | In order to describe transcription rates of an autoregulatory positive feedback system, we must look at the effect of activator/repressor binding on promoter activity. This proof works much in the same way as the repressor/promoter binding equation and it will lead us in the end to the Michaelis-Menten equation. We will start with the dissociation constant, K<sub>d</sub>, for activator/repressor binding: | ||
| + | [[Image:RA1.png|100px]] | ||
| + | |||
| + | Here, [R] represents the concentration of unbound repressor, [A] represents the concentration of unbound activator and [RA] represents the concentration of repressor/activator complexes. Instead of solving for the probability of unbound promoter as a function of repressor (as we did above), we now need to solve for the probability of bound repressor as a function of activator concentration. Once again, the probability that a repressor is bound to an activator is proportional to the rate of transcription and can be modified to describe promoter activity as a function of [A] by multiplying by the maximal rate of transcription. | ||
| + | |||
| + | We can modify the equation above by substituting [R] for [R<sub>total</sub>] - [RA] because the concentration of unbound repressor is equal to the total concentration of repressor minus the concentration of bound repressor: | ||
| + | |||
| + | [[Image:RA2.png|200px]] | ||
| + | |||
| + | Using simple algebra once again, we can solve for the probability of unbound repressor as a function of [A]: | ||
| + | |||
| + | [[Image:RA3.png|140px]] | ||
| + | |||
| + | Multiplying by the maximal rate of transcription, M, will yield an equation for transcription rate as a function of activator concentration: | ||
| + | |||
| + | [[Image:RA4.png|200px]] | ||
| + | |||
| + | Once again, it is true that the dissociation constant, K<sub>d</sub>, equals the activator concentration at which the transcription rate is half of its maximal value. The value of K<sub>d</sub> can, therefore, be easily determined experimentally. | ||
===The Hill Equation=== | ===The Hill Equation=== | ||
| Line 43: | Line 61: | ||
[[Image:linebreak.png]] | [[Image:linebreak.png]] | ||
| − | ==Cooperativity== | + | ==Cooperativity and Bistability== |
Show how Michaelis-Menton is the same as the hill equation when n=1 and then show what happens as n increases. (graph in book) | Show how Michaelis-Menton is the same as the hill equation when n=1 and then show what happens as n increases. (graph in book) | ||
[[Image:linebreak.png]] | [[Image:linebreak.png]] | ||
Revision as of 21:27, 29 November 2007
Main Page | Biological Designs | Mathematical Models | Toggle Switch | Hysteresis | Permanent Memory | Conclusions | References
Contents
|