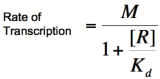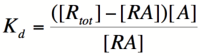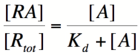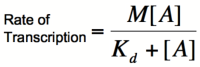Difference between revisions of "CellularMemory:Mathematical Models"
Wideloache (talk | contribs) |
Wideloache (talk | contribs) |
||
| Line 1: | Line 1: | ||
{{DeLoache Top}} | {{DeLoache Top}} | ||
| − | + | __NOTOC__ | |
=<center>Mathematical Models</center>= | =<center>Mathematical Models</center>= | ||
| Line 8: | Line 8: | ||
Note: the following mathematical analysis was developed based on a summary of the input function of a gene in ''An Introduction to Systems Biology: Design Principles of Biological Circuits'' [[CellularMemory:References |(Alon, pgs. 241-250)]]. | Note: the following mathematical analysis was developed based on a summary of the input function of a gene in ''An Introduction to Systems Biology: Design Principles of Biological Circuits'' [[CellularMemory:References |(Alon, pgs. 241-250)]]. | ||
| − | When dealing with gene activation and repression networks, such as those described in the common [[CellularMemory:Biological Designs |Biological Designs]] for synthetic cellular memory section of this paper, mathematical models are mainly used to model the transcription rate of a gene(s). Three common models that describe transcription rate as a function of repressor or activator are, in order of increasing complexity, the [http://en.wikipedia.org/wiki/Michaelis-Menten_kinetics Michaelis-Menten] model, the [http://en.wikipedia.org/wiki/Hill_equation Hill] model, and the [http://en.wikipedia.org/wiki/MWC_model Monod-Wymann-Changeux] model. Each of these | + | When dealing with gene activation and repression networks, such as those described in the common [[CellularMemory:Biological Designs |Biological Designs]] for synthetic cellular memory section of this paper, mathematical models are mainly used to model the transcription rate of a gene(s). Three common models that describe transcription rate as a function of repressor or activator are, in order of increasing complexity, the [http://en.wikipedia.org/wiki/Michaelis-Menten_kinetics Michaelis-Menten] model, the [http://en.wikipedia.org/wiki/Hill_equation Hill] model, and the [http://en.wikipedia.org/wiki/MWC_model Monod-Wymann-Changeux] model. Each of these models builds on the one preceding it to paint a clearer picture of how binding occurs between two or more molecules and how that binding affects transcription rates. |
| − | The Hill equation is used most often to model cellular memory networks. In order to describe how the Hill equation works, it is first helpful to examine a simpler model. Based on the two [[CellularMemory:Biological Designs |biological designs]] presented in the previous section, it can be reasoned that to mathematically model these designs, we must be able to describe the effect of repressor/promoter binding on transcription rates ([[CellularMemory:Biological Designs#Mutual Repression |mutual repression]]) and the effect of activator/repressor binding on transcription rates ([[CellularMemory:Biological Designs#Autoregulatory Positive Feedback |autoregulatory positive feedback]]). The two binding equations presented below do just that. | + | The Hill equation is used most often to model cellular memory networks. In order to describe how the Hill equation works, it is first helpful to examine a simpler model. Based on the two [[CellularMemory:Biological Designs |biological designs]] presented in the previous section, it can be reasoned that to mathematically model these designs, we must be able to describe the effect of repressor/promoter binding on transcription rates (for [[CellularMemory:Biological Designs#Mutual Repression |mutual repression]] designs) and the effect of activator/repressor binding on transcription rates (for [[CellularMemory:Biological Designs#Autoregulatory Positive Feedback |autoregulatory positive feedback]] designs). The two binding equations presented below do just that. |
===Repressor/Promoter Binding=== | ===Repressor/Promoter Binding=== | ||
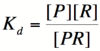
| − | Let's start by looking at the effect of repressor/promoter binding on transcription rate. The starting point for this proof is the dissociation constant for promoter and repressor binding. This constant, K<sub>d</sub>, measures the tendency for a repressor/promoter complex to fall apart into its two separate subunits. The value is determined by the binding affinity of the two molecules and is written as: | + | Let's start by looking at the effect of repressor/promoter binding on transcription rate. The starting point for this proof is the dissociation constant for promoter and repressor binding. This constant, K<sub>d</sub>, measures the tendency for a repressor/promoter complex to fall apart into its two separate subunits. The value of K<sub>d</sub> is determined by the binding affinity of the two molecules and is written as: |
[[Image:PR1.png|100px]] | [[Image:PR1.png|100px]] | ||
| − | where [P] represents the concentration of unbound promoter, [R] represents the concentration of unbound repressor and [PR] represents the concentration of promoter/repressor complexes. Our goal from here is to derive an equation that gives the probability of unbound promoter as a function of [R]. Because the probability of unbound promoters is proportional to the rate of transcription, we can easily modify the equation to give us the transcription rate as a function of [R] by multiplying by the maximal rate of transcription. | + | where [P] represents the concentration of unbound promoter, [R] represents the concentration of unbound repressor and [PR] represents the concentration of promoter/repressor complexes. Our goal from here is to derive an equation that gives the probability of unbound promoter as a function of [R]. Because the probability of unbound promoters (or, said differently, the percentage of promoters that are not bound to a repressor) is proportional to the rate of transcription, we can easily modify the equation to give us the transcription rate as a function of [R] by multiplying by the maximal rate of transcription. |
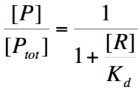
We can modify the equation above by substituting [P<sub>total</sub>] - [P] for [PR] because the concentration of unbound promoter plus the concentration of bound promoter equals the total promoter concentration: | We can modify the equation above by substituting [P<sub>total</sub>] - [P] for [PR] because the concentration of unbound promoter plus the concentration of bound promoter equals the total promoter concentration: | ||
| Line 31: | Line 31: | ||
[[Image:PR4.png|160px]] | [[Image:PR4.png|160px]] | ||
| − | Based on the equation above, it can be seen that the dissociation constant, K<sub>d</sub>, equals the repressor concentration at which the transcription rate is half of its maximal value. The value of K<sub>d</sub> can, therefore, be | + | Based on the equation above, it can be seen that the dissociation constant, K<sub>d</sub>, equals the repressor concentration at which the transcription rate is half of its maximal value. The value of K<sub>d</sub> can, therefore, easily be determined experimentally. |
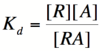
===Activator/Repressor Binding (The Michaelis-Menten Equation)=== | ===Activator/Repressor Binding (The Michaelis-Menten Equation)=== | ||
| Line 44: | Line 44: | ||
[[Image:RA2.png|200px]] | [[Image:RA2.png|200px]] | ||
| − | Using simple algebra once again, we can solve for the probability of | + | Using simple algebra once again, we can solve for the probability of bound repressor as a function of [A]: |
[[Image:RA3.png|140px]] | [[Image:RA3.png|140px]] | ||
| Line 52: | Line 52: | ||
[[Image:RA4.png|200px]] | [[Image:RA4.png|200px]] | ||
| − | Once again, it is true that the dissociation constant, K<sub>d</sub>, equals the activator concentration at which the transcription rate is half of its maximal value. The value of K<sub>d</sub> can, therefore, be | + | Once again, it is true that the dissociation constant, K<sub>d</sub>, equals the activator concentration at which the transcription rate is half of its maximal value. The value of K<sub>d</sub> can, therefore, easily be determined experimentally. |
===The Hill Equation=== | ===The Hill Equation=== | ||
Revision as of 00:24, 30 November 2007
Main Page | Biological Designs | Mathematical Models | Toggle Switch | Hysteresis | Permanent Memory | Conclusions | References
|