Davidson Missouri W/Solving the HPP in vivo
In 1994 Adleman developed a system to solve the Hamiltonian Path problem using DNA in vitro. We have implemented a bacterial system to solve Hamiltonian Path problems in vivo.
Contents
Overview
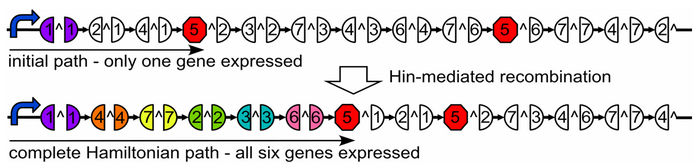
Our bacterial computer works by taking advantage of the Hin Recombinase protein and HixC sites to perform a "flipping" operation. By strategically placing HixC sites on a plasmid, along with reporter genes, we can simulate paths on a graph through flipping.
The Hin Recombinase/HixC System Revisited
Salmonella typhimurium is a bacterium which moves using flagella. Depending on its environment, it expresses different sets of surface proteins on its flagella. It is able to change this expression through the use of Hin Recombinase and Hix sites. The Hin Recombinase enzyme catalyzes the inversion of DNA that lies between a pair of Hix sites. By flipping DNA segments between Hix sites S. typhimurium can express alternate flagellar surface proteins.
Flipping Pancakes
In the 2006 iGEM competition, Davidson and Missouri Western used the Hix Recombinase/HixC to model a mathematical problem, called the Pancake Flipping problem. The problem is the following: given a stack of pancakes which are burnt on one side and golden on the other, and two spatulas, what is the minimum number of flips required to sort the stack by pancake size and with all burnt sides facing downwards?
Using mathematical models it is possible to compute these estimates for small stacks. However, adding pancakes to a stack increasing the number of possible permutations non-linearly. The number of possible stacks of n pancakes is equal to: 2^n (n!). Thus traditional computers are not well-suited for computations involving large pancake stacks.
However, it is possible to model pancake flipping using bacteria. If each pancake is given an identification number, along with a sign designating its orientation, then this can be stated equivalently using genes. Thus the following images show equivalent notations for pancake stacks.
Thus by taking advantage of this notation it is possible to use bacteria as computers to solve pancake-flipping problems.
The Hamiltonian Path Problem
Using the same flipping mechanism, we are trying to develop a bacterial computer which solves a new type of mathematical problem. Given a graph, a starting point, and an endpoint, is there a Hamiltonian path?
What is it?
A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none.