Mathematical Models
Mathematical modeling is an important component in the construction of rationally designed gene networks. The complexity of biological systems makes necessary the use of sophisticated mathematical models to accurately predict network functionality. Models are useful in tuning the individual components of a network to increase system robustness. They also provide a basis for comparison of experimental results with expected results, allowing researchers to test the validity of their assumptions.
Modeling Transcription Rates
Note: the following mathematical analysis was developed based on a summary of the input function of a gene in An Introduction to Systems Biology: Design Principles of Biological Circuits (Alon, pgs. 241-250).
When dealing with gene activation and repression networks, such as those described in the common Biological Designs for synthetic cellular memory section of this paper, mathematical models are mainly used to model the transcription rate of a gene(s). Three common models that describe transcription rate as a function of repressor or activator are, in order of increasing complexity, the Michaelis-Menten model, the Hill model, and the Monod-Wymann-Changeux model. Each of these model builds on the one preceding it to paint a clearer picture of how binding occurs between two or more molecules and how that binding affects transcription rates.
The Hill equation is used most often to model cellular memory networks. In order to describe how the Hill equation works, it is first helpful to examine a simpler model. Based on the two biological designs presented in the previous section, it can be seen that to mathematically model these designs, we must be able to describe the effect of repressor/promoter binding on transcription rates (mutual repression) and the effect of activator/repressor binding on transcription rates (autoregulatory positive feedback).
Repressor/Promoter Binding
Let's start by looking at the effect of repressor/promoter binding on transcription rate. The starting point for this proof is the dissociation constant for promoter and repressor binding. This constant, Kd, measures the tendency for a repressor/promoter complex to fall apart into its two separate subunits. The value is determined by the binding affinity of the two molecules and is written as:
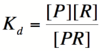
Here, [P] represents the concentration of unbound promoter, [R] represents the concentration of unbound repressor and [PR] represents the concentration of promoter/repressor complexes. Our goal from here is to derive an equation that gives the percentage of unbound promoters as a function of [R]. Because the percentage of unbound promoters is proportional to the rate of transcription, we can easily modify the equation to give us the transcription rate as a function of [R] by multiplying by the maximal rate of transcription.
We can modify the equation above by substituting [Ptotal] - [P] for [PR] because the concentration of unbound promoter plus the concentration of bound promoter equals the total promoter concentration:
Using simple algebra, we can now solve for the percentage of unbound promoter as a function of [R]:
Multiplying by the maximal rate of transcription, M, will yield an equation for transcription rate as a function of repressor concentration:
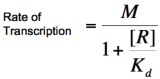
Based on the equation above, it can be seen that the dissociation constant, Kd, equals the repressor concentration at which the transcription rate is half of its maximal value. The value of Kd can, therefore, be easily determined experimentally.
Activator/Repressor Binding (The Michaelis-Menten Equation)
The Hill Equation
- Michaelis-Menton model doesn't take cooperativity into account.
- The Hill equation accounts for cooperativity of binding, but is not a completely accurate description at very low concentrations of repressor/activator.
- The Monod, Changeux, and Wymann model is the most accurate model of these three, but is not commonly used because of its increased complexity and the fact that the hill equation accurately describes most situations.
The Monod-Wymann-Changeux Equation
Cooperativity
Show how Michaelis-Menton is the same as the hill equation when n=1 and then show what happens as n increases. (graph in book)
Determining the Values of Funcational Parameters
Put text here.
Quantitative Part Characterization
Put text here.
<Previous Section | Next Section>
|
