Difference between revisions of "Davidson Missouri W/Mathematical Modeling"
Amshoecraft (talk | contribs) |
|||
| (22 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <center>[[Davidson | + | <center>[[Davidson Missouri W| <span style="color:red">Home</span>]] | [[Davidson Missouri W/Background Information| <span style="color:red">Background Information</span>]] | [[Davidson Missouri W/Solving the HPP in vivo| <span style="color:red">Current Project: Solving the Hamiltonian Path Problem ''in vivo''</span>]] | [[Davidson Missouri W/Mathematical Modeling| <span style="color:black">Mathematical Modeling</span>]] | [[Davidson Missouri W/Gene splitting| <span style="color:red"> Gene Splitting </span>]] | [[Davidson Missouri W/Controlling Expression| <span style="color:red"> Controlling Expression </span>]] | [[Davidson Missouri W/Traveling Salesperson Problem| <span style="color:red">Traveling Salesperson Problem</span> ]] | [[Davidson Missouri W/Backwards promotion and read-through transcription| <span style="color:red">Backwards Promotion and Read-Through Transcription</span>]] | [[Davidson Missouri W/Resources and Citations|<span style="color:red">Resources and Citations</span>]]</center> |
<hr> | <hr> | ||
| − | + | =Markov Chain Model For Flipping= | |
| − | + | '''Does starting orientation matter?''' | |
| − | + | Question: Will the order in which we place the edges in our E.coli computers affect the probability of us detecting a Hamiltonian Path? | |
| − | + | Our mathematical reasoning relies on the fact that the Hin/HixC DNA recombination system makes a large number of flips and for any one flip there is some element of chance that dictates which Hix sites are chosen to flip. | |
| − | + | Answer: We developed a Markov Chain model that takes every signed permutation of edges as a state and the connections between these states are found and categorized by our Matlab programs by both the number of edges that need to be flipped to move between those states and categorized by which specific edge needed to be flipped. Further, our Matlab programs creates a transition matrix based on the weights a user enters to bias the probabilities of making different kinds of flips. | |
| − | + | Once this transition matrix is generated we then compute, for each possible starting state, the probability of that starting state transitioning to any of the solved states after x flips given the biasing of different types of flips. When our Markov Chain model is run for more than 2 edges we always observe a convergence of these probabilities no matter what bias we apply. This shows that starting orientation does not matter since the probability of being solved after a large number of flips is the same for each starting orientation. | |
| − | |||
| − | |||
| − | + | This begs the question: what is a large number of flips? Mostly we observe that this convergence occurs in the first 20 flips for three edges and only for very extreme probabilities does this convergence occur after 60 flips. However, as the number of edges increase we can expect this convergence to occur later. This does not appear to be a problem. Our flipping mechanism flips edges very quickly, so quickly that it is hard to measure. Additionally, the diameter of our transition diagrams increases linearly with the number of edges so there is no reason to believe that the number of flips to convergence would increase at more than a linear pace. | |
| − | |||
| − | |||
| − | |||
| − | + | [[Image:MarkovChaingraph4nod3edg.jpg]] | |
| − | |||
MATLAB programs that we developed using Markov Chains | MATLAB programs that we developed using Markov Chains | ||
| Line 36: | Line 30: | ||
| − | |||
| − | + | <br> | |
| + | = True Positives / False Positives = | ||
| − | + | [[Image:5_node-wiki.jpg]] | |
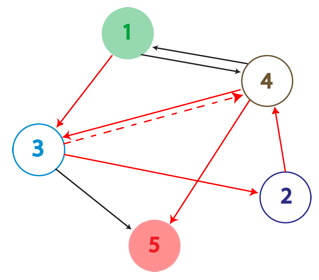
| − | + | True positives are the Hamiltonian Path represented in the above graph with solid red arrows and below as the PCR Fragment Length where the edges after the Hamiltonian path can be arranged in any order. | |
| − | + | [[Image:True_positive.jpg]] | |
| − | + | A false positive is represented in the graph above with the solid red arrows and the dotted red arrow showing a "teleport" which causes this path to be a false positive. Teleporting occurs when an edge entering a node is followed by an edge leaving from a different node. Below you can see an extra edge that is highlighted, representing the teleport. In this example, the edge from 4 to 3 is followed by the edge from 4 to 5. | |
| − | + | [[Image:Fpospic.jpg]] | |
| − | + | ||
| + | MATLAB programs used to find the false positives: | ||
| − | |||
| − | + | [http://gcat.davidson.edu/iGEM07/For_Missouri_Western/fpVTgraph.m 1. False positives for the 8 edge / 5 node graph shown above] | |
| + | |||
| + | true positives = 384 | ||
| + | false positives = 1,362 | ||
| + | |||
| + | [http://gcat.davidson.edu/iGEM07/For_Missouri_Western/davidson85Iweighter.m 2. Counter Program for the 8 edge / 5 node graph] | ||
| + | |||
| + | [http://gcat.davidson.edu/iGEM07/For_Missouri_Western/adelman147.m 2. Adelman's false positives with 14 edges / 7 nodes] | ||
| + | |||
| + | true positives = 10,321,920 | ||
| + | false positives = 168,006,848 | ||
| + | |||
| + | [http://gcat.davidson.edu/iGEM07/For_Missouri_Western/fpweighter.m 3. Counter Program for Adelman's False Positives] | ||
| + | |||
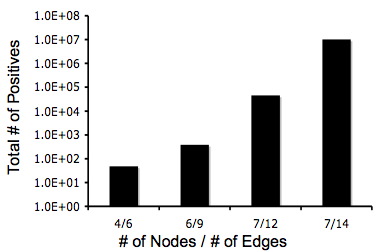
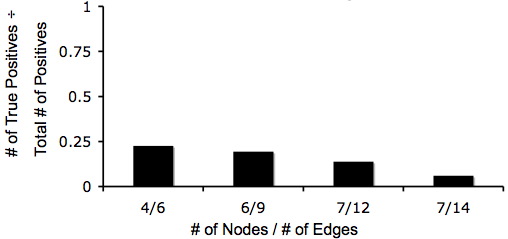
| − | + | Below are two graphs that show how quickly graphs can be complex so it makes the Hamiltonian Path harder to detect. Also, from these graphs you can tell that even though the graphs are very complex that there is still a 5% change of detecting a Hamiltonian Path or a true positive. | |
| − | + | [[Image:Positivenodedg.jpg]] [[Image:Truetotalpos.jpg]] | |
| − | + | =Possion Model For the Number of Plasmids= | |
| − | |||
| − | + | '''How many E.coli computers?''' | |
| − | + | Question: If a Hamiltonian Path exists in the graph, how many E.coli computers do we need to have working on the problem to be highly confident that at least k of our computers will find it? | |
| − | + | Our mathematical reasoning relies on the fact that the Hin/HixC DNA recombination system makes a large number of flips and for any one flip there is some element of chance that dictates which Hix sites are chosen to flip. Note: This has now been shown to be true but it needs to be stated that our math relies on it. | |
| − | + | If this is the case then our E.coli computers will be equally likely to have flipped into each possible signed ordering of edges by the time we screen our results. For more details on this see our section answering the question does starting orientation matter? | |
| − | + | We can use a cumulative Poisson distribution to answer this question. | |
| − | |||
| − | + | Answer: The Poisson distribution gives the probability of k occurrences when the expected number of occurrences is λ as (e^-λ)*(λ^k)/(k!). By taking 1 minus the sum of the Poisson probabilities from 0 to k-1 we get the cumulative probability of at least k occurrences. | |
| − | + | For example examine the Adleman graph. It has 14 edges and 7 nodes. This means that a Hamiltonian Path is represented in our plasmids by 6 edges in the proper order and orientation followed by 8 edges in any order and in any orientation. | |
| − | + | Thus there are 8!*2^8 orderings that are true positives and 14!*2^14 possible orderings. The probability of any one plasmid holding a true positive is then 8!*2^8 / 14!*2^14. If we have m plasmids, λ= m*8!*2^8 / 14!*2^14. | |
| − | + | Now if we want to know the probability of at least one true positive in m plasmids, we use k =1 and the expression becomes 1-(e^-(m*8!*2^8/14!*2^14)) as the summand collapses to the case where k=0 and (λ^0)/(0!) then equals 1. | |
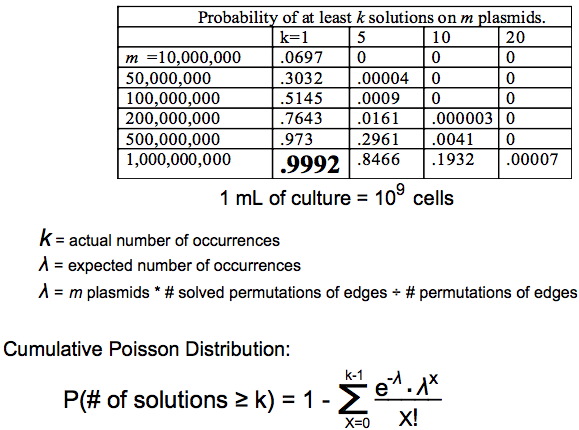
| − | + | We can then solve for m depending on how confident we want to be. If we use | |
| + | m=1 billion plasmids then we expect to find the Hamiltonian Path when one exists 99.92% of the time. | ||
| − | + | 1 billion E.coli computers fit conveniently into 1 mL of culture. | |
| − | |||
| − | + | Using this statistical method we made a chart showing the probability of finding true positives based on the number of plasmids. | |
| − | + | [[Image:Plasmidsneeded.jpg]] | |
Latest revision as of 18:45, 9 August 2007
Markov Chain Model For Flipping
Does starting orientation matter?
Question: Will the order in which we place the edges in our E.coli computers affect the probability of us detecting a Hamiltonian Path?
Our mathematical reasoning relies on the fact that the Hin/HixC DNA recombination system makes a large number of flips and for any one flip there is some element of chance that dictates which Hix sites are chosen to flip.
Answer: We developed a Markov Chain model that takes every signed permutation of edges as a state and the connections between these states are found and categorized by our Matlab programs by both the number of edges that need to be flipped to move between those states and categorized by which specific edge needed to be flipped. Further, our Matlab programs creates a transition matrix based on the weights a user enters to bias the probabilities of making different kinds of flips.
Once this transition matrix is generated we then compute, for each possible starting state, the probability of that starting state transitioning to any of the solved states after x flips given the biasing of different types of flips. When our Markov Chain model is run for more than 2 edges we always observe a convergence of these probabilities no matter what bias we apply. This shows that starting orientation does not matter since the probability of being solved after a large number of flips is the same for each starting orientation.
This begs the question: what is a large number of flips? Mostly we observe that this convergence occurs in the first 20 flips for three edges and only for very extreme probabilities does this convergence occur after 60 flips. However, as the number of edges increase we can expect this convergence to occur later. This does not appear to be a problem. Our flipping mechanism flips edges very quickly, so quickly that it is hard to measure. Additionally, the diameter of our transition diagrams increases linearly with the number of edges so there is no reason to believe that the number of flips to convergence would increase at more than a linear pace.
MATLAB programs that we developed using Markov Chains
True Positives / False Positives
True positives are the Hamiltonian Path represented in the above graph with solid red arrows and below as the PCR Fragment Length where the edges after the Hamiltonian path can be arranged in any order.
A false positive is represented in the graph above with the solid red arrows and the dotted red arrow showing a "teleport" which causes this path to be a false positive. Teleporting occurs when an edge entering a node is followed by an edge leaving from a different node. Below you can see an extra edge that is highlighted, representing the teleport. In this example, the edge from 4 to 3 is followed by the edge from 4 to 5.
MATLAB programs used to find the false positives:
1. False positives for the 8 edge / 5 node graph shown above
true positives = 384 false positives = 1,362
2. Counter Program for the 8 edge / 5 node graph
2. Adelman's false positives with 14 edges / 7 nodes
true positives = 10,321,920 false positives = 168,006,848
3. Counter Program for Adelman's False Positives
Below are two graphs that show how quickly graphs can be complex so it makes the Hamiltonian Path harder to detect. Also, from these graphs you can tell that even though the graphs are very complex that there is still a 5% change of detecting a Hamiltonian Path or a true positive.
Possion Model For the Number of Plasmids
How many E.coli computers?
Question: If a Hamiltonian Path exists in the graph, how many E.coli computers do we need to have working on the problem to be highly confident that at least k of our computers will find it?
Our mathematical reasoning relies on the fact that the Hin/HixC DNA recombination system makes a large number of flips and for any one flip there is some element of chance that dictates which Hix sites are chosen to flip. Note: This has now been shown to be true but it needs to be stated that our math relies on it.
If this is the case then our E.coli computers will be equally likely to have flipped into each possible signed ordering of edges by the time we screen our results. For more details on this see our section answering the question does starting orientation matter?
We can use a cumulative Poisson distribution to answer this question.
Answer: The Poisson distribution gives the probability of k occurrences when the expected number of occurrences is λ as (e^-λ)*(λ^k)/(k!). By taking 1 minus the sum of the Poisson probabilities from 0 to k-1 we get the cumulative probability of at least k occurrences.
For example examine the Adleman graph. It has 14 edges and 7 nodes. This means that a Hamiltonian Path is represented in our plasmids by 6 edges in the proper order and orientation followed by 8 edges in any order and in any orientation.
Thus there are 8!*2^8 orderings that are true positives and 14!*2^14 possible orderings. The probability of any one plasmid holding a true positive is then 8!*2^8 / 14!*2^14. If we have m plasmids, λ= m*8!*2^8 / 14!*2^14.
Now if we want to know the probability of at least one true positive in m plasmids, we use k =1 and the expression becomes 1-(e^-(m*8!*2^8/14!*2^14)) as the summand collapses to the case where k=0 and (λ^0)/(0!) then equals 1.
We can then solve for m depending on how confident we want to be. If we use m=1 billion plasmids then we expect to find the Hamiltonian Path when one exists 99.92% of the time.
1 billion E.coli computers fit conveniently into 1 mL of culture.
Using this statistical method we made a chart showing the probability of finding true positives based on the number of plasmids.