Difference between revisions of "Davidson Missouri W/Solving the HPP in vivo"
(→The Hamiltonian Path Problem) |
|||
| Line 4: | Line 4: | ||
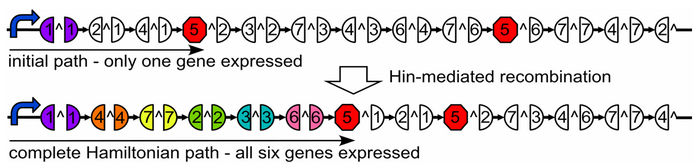
A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none. Given a graph, a starting point, and an endpoint, is there a Hamiltonian path? | A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none. Given a graph, a starting point, and an endpoint, is there a Hamiltonian path? | ||
| − | == | + | We solve our problem by transforming ''E. coli'' cells with specially engineered plasmids. |
| + | |||
| + | ==Designing a Plasmid== | ||
| + | Our plasmid consists of reporter genes and ''HixC'' sites. ''HixC'' sites are placed within the coding regions of our reporter genes. The reporter genes are joined in such a way as to represent a graph. Each reporter gene represents a node, and the connection of two reporter genes together without any ''HixC'' sites in between represents an edge. | ||
| − | |||
[[Image:HamiltonianGraph.PNG|thumb|700px|center|]] | [[Image:HamiltonianGraph.PNG|thumb|700px|center|]] | ||
| − | + | ==Developing Nodes== | |
=The Traveling Salesman Problem= | =The Traveling Salesman Problem= | ||
Revision as of 23:15, 6 July 2007
Using the same flipping mechanism, we are trying to develop a bacterial computer which solves a new type of mathematical problem, the Hamiltonian Path problem
Contents
The Hamiltonian Path Problem
A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none. Given a graph, a starting point, and an endpoint, is there a Hamiltonian path?
We solve our problem by transforming E. coli cells with specially engineered plasmids.
Designing a Plasmid
Our plasmid consists of reporter genes and HixC sites. HixC sites are placed within the coding regions of our reporter genes. The reporter genes are joined in such a way as to represent a graph. Each reporter gene represents a node, and the connection of two reporter genes together without any HixC sites in between represents an edge.