Difference between revisions of "Davidson Missouri W/Solving the HPP in vivo"
(→The Hamiltonian Path Problem) |
(→The Hamiltonian Path Problem) |
||
| Line 2: | Line 2: | ||
=The Hamiltonian Path Problem= | =The Hamiltonian Path Problem= | ||
| − | A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none. Given a graph, a starting point | + | A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none. Given a graph, a starting point and an endpoint, does it contain a Hamiltonian path? |
We solve our problem by transforming ''E. coli'' cells with specially engineered plasmids. | We solve our problem by transforming ''E. coli'' cells with specially engineered plasmids. | ||
| Line 12: | Line 12: | ||
==Developing Nodes== | ==Developing Nodes== | ||
| + | We represent the graph's nodes with reporter genes. In order to allow for flipping, we must insert ''HixC'' sites within the coding regions of our reporter genes. We call this process [[Gene splitting|''gene splitting'']]. If our reporter gene tolerates a ''HixC'' insertion then we can use it as a node on our graph. | ||
=The Traveling Salesman Problem= | =The Traveling Salesman Problem= | ||
Revision as of 21:30, 7 July 2007
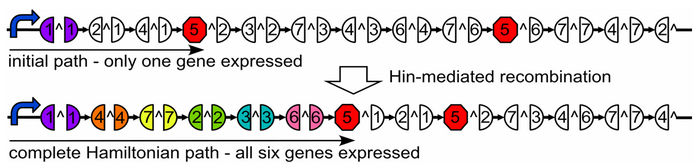
Using the same flipping mechanism, we are trying to develop a bacterial computer which solves a new type of mathematical problem, the Hamiltonian Path problem
Contents
The Hamiltonian Path Problem
A Hamiltonian Path is a trip through a graph which visits each node exactly once. A graph may have multiple Hamiltonian Paths, only one, or even none. Given a graph, a starting point and an endpoint, does it contain a Hamiltonian path?
We solve our problem by transforming E. coli cells with specially engineered plasmids.
Designing a Plasmid
Our plasmid consists of reporter genes and HixC sites. HixC sites are placed within the coding regions of our reporter genes. The reporter genes are joined in such a way as to represent a graph. Each reporter gene represents a node, and the connection of two reporter genes together without any HixC sites in between represents an edge.
Developing Nodes
We represent the graph's nodes with reporter genes. In order to allow for flipping, we must insert HixC sites within the coding regions of our reporter genes. We call this process gene splitting. If our reporter gene tolerates a HixC insertion then we can use it as a node on our graph.