Literature Read and Summaries

Papers to Read

• Isaacs FJ et al. Prediction and measurement of an autoregulatory genetic module
• Atkinson MR et al. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli
• Zhou TS, Chen LN, Aihara K. Molecular communication through stochastic synchronization induced by extracellular fluctuations
• McMillen D, Kopell N, Hasty J, Collins JJ. Synchronizing genetic relaxation oscillators by intercell signaling.
• Stricker 2008
• Jones T, Gill CO, McMullen LM. Behaviour of log-phase Escherichia coli at temperatures near the minimum for growth.

Works Read

• Acar M, Becskei A, van Ourdenaarden A. (2005). Enhancement of cellular memory by reducing stochastic transitions. Nature 435: 228 – 32.
• Becskei A, Seraphin B, Serrano L. (2001). Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion. EMBO 20: 2528 – 35.
• Cooper S. (1989). The constrained hoop: an explanation of the overshoot in cell length during a shift-up of Escherichia coli. J Bacteriol 171: 5239 – 43.
• Cox CD, Peterson GD, Allen MS, Lancaster JM, McCollum JM, Austin D, Yan L, Sayler GS, Simpson ML. (2003). Analysis of noise in quorum sensing. OMICS 7: 317 – 34.
• Danchin A. (2009). Natural selection and immortality. Biogerontology 10: 503 – 16.
• Danino T, Mondragon-palomino O, Tsimring L, Hasty J. (2010). A synchronized quorum of genetic clocks. Nature 463: 326 – 30.
• Engberg B, Hjalmarsson K, Nordstrom K. (1975). Inhibition of cell division in Escherichia coli K-12 by the R-factor R1 and copy mutants of R1. J Bacteriol 124: 633 – 40.
• Freed NE, Silander OK, Stecher B, Böhm A, Hardt WD, Ackermann M. (2008). A simple screen to identify promoters conferring high levels of phenotypic noise. PLoS Genet 4(12): e1000307.
• Goksor M, Diez A, Enger J, Hanstorp D, Nystrom T. (2003). Analysis of molecular diffusion in ftsK cell-division mutants using laser surgery. EMBO Reports 4: 867 – 71.
• Gustafsson P, Nordstrom K. (1975). Random replication of the stringent plasmid R1 in Escherichia coli K-12. J Bacteriol 123: 443 – 48.
• Holtz WJ, Keasling JD. (2010). Engineering static and dynamic control of synthetic pathways. Cell 140: 19 – 23.
• Isaacs FJ, Hasty J, Cantor CR, Collins JJ. (2003). Prediction and measurement of an autoregulatory genetic module. PNAS 100: 7714 – 19.
• Jain V, Kumar M, Chatterji D. (2006). ppGpp: stringent response and survival. J. Microbiol 44: 1 – 10.
• Jishage M, Kvint K, Shingler V, Nystrom T. (2002). Regulation of σ factor competition by the alarmone ppGpp. Genes Dev 16:1260 – 70.
• Kaern M, Elston TC, Blake WJ, Collins JJ. (2005). Stochasticity in Gene expression: from theories to phenotypes. Nature Rev Genet 6: 451–64.
• Nystrom, T. (2002). Aging in bacteria. Curr Opinon Microbiol 5: 596 – 601.
• Orgel LE. (1963). The maintenance of the accuracy of protein synthesis and its relevance to ageing. Biochem 49: 517 – 21.
• Pin C, Rolfe MD, Muñoz-Cuevas M, Hinton JC, Peck MW, Walton NJ, Baranyi J. (2009). Network analysis of the transcriptional pattern of young and old cells of Escherichia coli during lag phase. BMC Syst Biol 16,3: 108.
• Qi B, Chi YM, Lo HK, Qian L. (2010). High-speed quantum random number generation by measuring phase noise of a single-mode laser. Optics Letters 35: 312 – 14.
• Srivatsan A, Wang JD. (2008). Control of bacterial transcription, traslation and replication by (p)ppGpp. Curr Opin Microbiol 11: 100 – 05.
• Stewart EJ, Madden R, Paul G, Taddei F. (2005). Aging and death in an organism that reproduces by morphologically symmetric division. PLoS Biol 3(2): e45.
• Sturgeon JA, Ingram LO. (1978). Temperature conditional cell division mutants of Escherichia coli. J Bacteriol 133: 256 – 64.
• Summers J, Litwin S. (2006). Examining the theory of error catastrophe. J Virol 80: 20 – 26.
• Vilar JMG, Kueh HY, Barkai N, Leibler S. (2002). Mechanisms of noise-resistance in genetic oscillators. PNAS 5988 – 92.
• Wang J, Zhang J, Yuan Z, Zhou T. (2007). Noise-induced switches in network systems of the genetic toggle switch. BMC Sys Biol 1: 50.
• Zhou T, Chen L, Wang R, Aihara K. (2004). Intercellular communication induced by random fluctuations. Genome Informatics 15: 223 – 33.

Review Summaries

Kaern M, Elston TC, Blake WJ, Collins JJ. (2005). Stochasticity in Gene expression: from theories to phenotypes. Nature Rev Genet 6: 451–64.

This review gives an introduction to the theoretical mechanisms of noise in gene expression levels in genotypically identical cells. In modeling stochastic behaviour, you need to focus on random formation and decay of single molecules and multi-component complexes. So a major part of research on noise illustrates new techniques developed to do single-cell analyses. It would be beneficial to think of ways that I could use multi-component complexes in order to enlarge the focus from a single molecule to a larger complex. For example, I think measuring something like hemoglobin could show more dramatic measurements in noise variation because it requires more than a single molecule to make a functional unit.

Gene expression noise is defined as the relative deviation from the average, measuring as the standard deviation divided by the mean. Kaern covers some factors that influence the amount of noise in gene expression. The ‘finite-number effect’ is the most notable manifestation of noise – with a smaller number of molecules affecting protein abundance in a compartment, noise increases. Varying the rate of transcription causes a greater change in gene expression noise than varying the translational efficiency (the number of proteins per mRNA molecule). It’s predicted that the rate of transcription should be most sensitive to variation in the regulatory signal at intermediate induction levels. Mostly factors are addressed to learn how to minimize noise, but it could be interesting to see how to maximize noise and a potential application.

In synthetic systems, longer cascades have more noise because there are more steps. Negative feedback loops provide a noise-reduction mechanism, and may minimize noise in downstream processes too. But Kaern also notes that negative feedback can also have a destabilizing effect if it involves a time delay (1) Positive feedback generally amplifies fluctuations and population heterogeneity, and possibly yielding bimodal population distributions. (2) I thought mechanisms causing distinct phenotypic consequences would be interesting by using noise to create two different and useful cell populations, perhaps that somehow function together. One oscillatory network design (3) consisted of an activator and repressor allowing dampened but synchronized oscillations; Kaern here notes that fluctuations in gene expression can in theory cause the emergence of oscillations that would not appear otherwise. Finally, the review concludes with biological significance of stochasticity. It is particularly beneficial to microbial cells that need to adapt efficiently to sudden environmental changes – a mechanism for “sampling” distinct physiological states without genetic mutation. I’d like to come up with some synthetic use and way to construct “sampling”.

Interesting / Useful Papers Cited:

1. Monk NA. Oscillatory expression of Hes1, p53, and NF-KB driven by transcriptional time delays
2. Isaacs FJ et al. Prediction and measurement of an autoregulatory genetic module
3. Atkinson MR et al. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli

Nystrom, T. (2002). Aging in bacteria. Curr Opinon Microbiol 5: 596 – 601.

This (review) paper supports an idea of aging as a trade-off between reproduction and survival activities. “Aging” in E. coli is seen as the point at which bacterial cells enter a non-proliferating state (stationary phase) due to nutrient depletion, during which they gradually lose their ability to recover and reproduce, and eventually lose membrane integrity and other vital activities – conditional senescence. Growth-arrested cells are resistant to a large amount of secondary stresses (stasis-induced crossprotection), due to a transcription factor sigma S (and E). Mutants lacking sigma S exhibit senescence faster during growth arrest and have more oxidative damage. But there is a selective advantage for E. coli to lose sigma S when growing under non-stressful conditions. Cells grow faster with increased rate of reproduction, but have weaker resistance against starvation-induced stasis.

Sigma factors compete for RNA polymerase binding – sigma 70 for survival activities, sigma S for maintenance & crossprotection – Can this be useful? (Think of something where competition is useful. The limited amount of RNA polymerase would lean towards the idea of finite number effect in stochastic behaviour, but the behaviour must somehow be stochastic, not directed by stress level because…) …The competition between sigma factors has been shown to be highly regulated and dictated by nutritional quality of the environment and the nucleotide ppGpp Is there noise in the movement of RNA polymerase after it binds to DNA? So that maybe if the sigma factor binding sites were facing opposite ways RNA pol could accidentally move one way or the other? ppGpp primes the RNA polymerase in accordance with the env’tal signals, so that when ppGpp levels are low this signals nutritional status is favorable and directs polymerase toward sigma 70 genes. When levels are high, polymerase is directed toward sigma S (? – says 70, but that doesn’t make sense).

The article then mentions different theories of aging – one brings up something related to noise – Orget introduced the concept that for an error feedback loop in macromolecular synthesis, this could cause an irreversible increase in error levels, leading to an error catastrophe. This may actually be the opposite of what we want, but it would be an interesting thing to anticipate in a synthetic system – instead of working to minimize noise another way, get a very clean digital system by amplifying the noise until it’s out of control and all of those cells die.

Carbonylation of proteins causes the rapid degradation of them, in case that’s useful later, stochasticity by degradation rate/frequency.

The paper also presents a hypothesis that reduced translational fidelity of growth-arrested cells is probably from ribosomes being starved for charged tRNAs – we could do something with tRNAs to cause a noisy system.

Summers J, Litwin S. (2006). Examining the theory of error catastrophe. J Virol 80: 20 – 26.

This review explains the error catastrophe theory and gives a simple model based on a mathematical model. Error catastrophe has been used as a theoretical basis for treating viral infection, with drugs that push the error rate for the viral genome beyond a viable threshold. Eigen and Schuster originally came up with the error catastrophe model – also a mathematical model. The model presented here does not give a simulation on how to initiate error accumulation. Here, the conclusion is “unlike real life, mutagenesis in the error catastrophe model does not produce any lethal mutations but only limited deleterious mutations. This assumption of the model is essential for generating error catastrophy at a threshold error rate.”

This isn’t very encouraging. If there is no error threshold in real life, that may mean you could not tune the system to a desired noise threshold – or you could, but by mutagenesis, it would either be immediately lethal (not a problem) or not lethal for generations while errors accumulate (is a problem) which is not exactly a controllable process. Control would have to come from the error inducer.

Srivatsan A, Wang JD. (2008). Control of bacterial transcription, traslation and replication by (p)ppGpp. Curr Opin Microbiol 11: 100 – 05.

This is a review about guanosine tetra- and pentaphosphate, which accumulate rapidly in E. coli (and other bacteria and plants) starved for amino acids, inhibiting synthesis of rRNAs and tRNAs in order to shut down growth and trigger adaptive responses to stress. The starvation response is called stringent response, but ppGpp is probably involved in growth as well. “The ability of cells to produce these small nts profoundly affects translation, and is important for virulence induction, differentiation, and persistence…its ability to modify global cellular metabolism nearly instantaneously in response to changes in the env’t” – that may be a little too critical of an element to mess with. RelA and SpoT proteins synthesize ppGpp and hydrolyze it back to GDP/GTP.

ppGpp-mediated transcriptional re-programming encompasses several hundred genes in each organism. These changes in gene expression involve interactions with RNAP, promoters, sigma factors, and a cofactor called DksA. DksA is a suppressor of dnaK, and is required for the in vivo effect of ppGpp on transcription from both rRNA and amino acid synthesis promoters. The inherent kinetics of the promoters determine which are upregulated and downregulated by ppGpp – rRNA promoters have GC-rich sequences upstream, and amino acid biosynthesis promoters have AT-rich sequences that binds optimally to the sigma factor subunit of RNAP. Altogether, ppGpp is proposed to help maintain genomic integrity “by resolving conflects between replication and transcription”; this applies to ppGpp in other bacteria like B. subtilis as well.

So my main thought about this review is that it would be very risky/difficult to work with ppGpp, but it does not mean it’s impossible I suppose.

Jain V, Kumar M, Chatterji D. (2006). ppGpp: stringent response and survival. J. Microbiol 44: 1 – 10.

This is another review about ppGpp that discusses its accumulation during nutritional response resulting in repression of rRNA and tRNA species. This paper focuses on pathogenic microorganisms including Myxococcus xanthus (the first species discovered to have msDNA I think), Pseudomonas aeruginosa and Campylobactor jejuni, Mycobacterium, Salmonella, Listeria, etc.

ppGpp overall has a wide effect on cellular physiology. Overproduction of ppGpp can cause change in colony morphology, and its production induces sporulation in M. xanthus. ppGpp is also involved in quorum sensing and symbiosis. Increase in ppGpp levels corresponded with induction of virulence genes in pathogens including Salmonella, Vibrio cholerae, Pseduomonas, etc.

So this paper emphasizes that ppGpp is a very common very critical element in many microorganisms. This makes it difficult to control in a synthetic system.

Holtz WJ, Keasling JD. (2010). Engineering static and dynamic control of synthetic pathways. Cell 140: 19 – 23.

This review / essay talks about how most engineered systems do not sense changes in pathway output or cellular environment to influence gene expression; this is a static system. “Improvements in yield or productivity could be achieved if the pathway has the capacity to monitor and respond to the cell’s growth phase and density”. This would be a dynamic system. Coupling sensory inputs with control devices makes them dynamically controlled. We could possibly do that with noise – sense the env’t and optimize accordingly.

Article Summaries

Isaacs FJ, Hasty J, Cantor CR, Collins JJ. (2003). Prediction and measurement of an autoregulatory genetic module. PNAS 100: 7714 – 19.

In this paper, the authors constructed a positive feedback module in E. coli using the bacteriophage lambda genetic switch mechanism. “Feedback loops…can include…the rapid switching between two or more outputs, and even the suppression or amplification of noise.” They simplified the lambda phage system down to the OR – right operator in the promoter – and the cI gene which codes for a temperature sensitive repressor protein. GFP was placed downstream of cI under the same promoter to be expressed together. They varied the temperature of the environment to tune the stability of the repressor, varying the degree of activation portion of the positive feedback loop. By destabilizing the repressor, they hoped to control the positive feedback loop.

They found, however, that noise plays a significant role in the tuning of the positive feedback loop. As they increased the temperature to 39 degrees C, the monostable state split into two coexisting stable populations, and remained that way through 40 degrees. So stochasticity in the destabilization of the repressor either causes the cell to amplify the amount of GFP by a positive feedback loop, or causes a minimal amount of GFP – “trademark bistability of the positive feedback architecture”. In the discussion, the author also mentioned differing the plasmid copy numbers (since this noise is a finite number effect). So to make a noisier system, we could use a smaller abundance of repressor.

So from this paper, I could explore making a similar system in which we utilize noise by destabilizing a repressor-like element in order to make bistable cell populations…for something.

Becskei A, Seraphin B, Serrano L. (2001). Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion. EMBO 20: 2528 – 35.

In this paper, the authors worked with S. cerevisiae. The introduction of this paper gives a good clear background for positive feedback loops / bistability – might be useful in the future for a write-up. The point of this paper was to see if positive feedback generates a binary response in eukaryotic circuits like it does in prokaryotic. In this construct, they used a promoter (?) CYC1 to regulate GFP and an activator (?) rtTA, which can be induced with doxycycline (rtTA is being induced I believe, not the promoter). rtTA binds to CYC1 which creates a positive feedback loop (don’t understand the mechanism so much here). This circuit was used in a plasmid and in the chromosome, and both locations caused a bimodal GFP distribution. Both the induction level and the gene copy number contributed to the activation level. Cells randomly turned on GFP production, switching from off to on (but not switching the other way). So this paper also observed bistability with a positive feedback loop, but the system does not stochastically switch both ways (not a toggle switch). The switching time itself is the random part.

So from this paper, I learned that positive feedback loops seem inherently bistable in their output, and the output could be a direct product of noise. Copy number and induction level is important. We could make a device to perhaps make two different populations, as some useful cell differentiation.

Vilar JMG, Kueh HY, Barkai N, Leibler S. (2002). Mechanisms of noise-resistance in genetic oscillators. PNAS 5988 – 92.

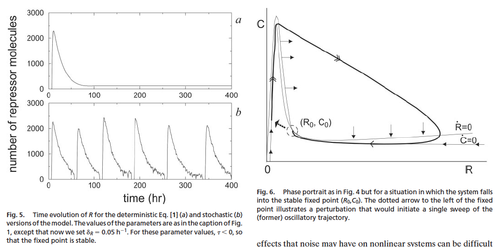
This paper was really cool, but very mathematical (could figure some out if refreshed on Mathematical Methods for Scientists info) – quite hard to read, I skimmed most. Gist: Authors created a simulation of a genetic oscillator using mathematical models. They made a deterministic model and a stochastic model modifying the deterministic model. Their point in making the deterministic model was to study strategies of minimizing noise (compared to the stochastic model). But interestingly they found that parameter values to produce a stable state in the deterministic model continue to produce oscillation cycles in the stochastic model. So theoretically, the presence of noise can actually initiate a new cycle and drive an oscillatory circuit. Noise here was due to finite number effect, with respect to repressor degradation rate and the activator-repressor complex.

So this paper is exciting because it models a way in which one can take advantage of cellular noise to perform functions not possible by deterministic means. So constructing a noise-driven oscillator is an idea. On a population scale though, the application would need to take into account that all cells would not be oscillating together, and stop oscillating at different times.

Wang J, Zhang J, Yuan Z, Zhou T. (2007). Noise-induced switches in network systems of the genetic toggle switch. BMC Sys Biol 1: 50.

I didn’t like this paper much; it was very difficult to read because of the degree of math and the grammar – it may have been translated. But it was another article about bistability and switches. Here, they elucidate the single and coupled genetic toggle switch systems in E. coli through mathematical modeling of the Gardner single toggle switch (2 repressors facing opposite ways) and a multicellular toggle switch with quorum sensing.

In the Gardner single toggle switch, the degradation rate of the repressors can induce successive switching between two stable steady states. This is the design of the Gardner switch, so the noise is governing the timing I believe, based on Figure 2A. In the multicellular gene regulatory network, the system acts as a toggle switch and uses an intercellular signaling mechanism to couple between cells. The signalizing system is Lux operon, in which the autoinducer (AI) made by LuxI diffuses across the cell membrane. One notable thing I did get out of this part was that noise in such a signaling system can make noise more notable, and lead to a robust collective rhythm. So noise in quorum sensing may be a very useful factor to consider, and perhaps using the Lux operon for signaling or positive feedback.

Articles Cited:

1. Zhou TS, Chen LN, Aihara K. Molecular communication through stochastic synchronization induced by extracellular fluctuations
2. McMillen D, Kopell N, Hasty J, Collins JJ. Synchronizing genetic relaxation oscillators by intercell signaling.

Cox CD, Peterson GD, Allen MS, Lancaster JM, McCollum JM, Austin D, Yan L, Sayler GS, Simpson ML. (2003). Analysis of noise in quorum sensing. OMICS 7: 317 – 34.

It’s shown especially by the bacteriophage lambda system that noise is pivotal in gene circuitry (pathway depends on the chance early and strong production of cI). Like the lambda switch, bacterial quorum sensing systems operate in a population and contain a bistable switching element, so it’s likely noise plays a pivotal role in QS too. For their simulation, they used the Lux regulon. The threshold in the Lux system is the concentration of the LuxR-AI (autoinducer) complex required to initiate the state transition (not induced → induced). The noise in the LuxR-AI complex increases as the threshold is approached. Once the threshold is reached, the production of LuxI increases rapidly with a small AI increase. Some cells would reach the threshold earlier than others because of the noise here. These early switching cells reinforce their behavior throughout the population by production of more AI (helping other cross the threshold). The authors hypothesize that although this does not seem like a dynamic noise system, there is a benefit in distributing this additional positive feedback throughout the population, versus in individual cells. By doing so, the noise acting as positive feedback distributed may act to ensure the operation of the QS circuit even if other organisms or processes are actively interfering with the signal system. This last point (underlined) sounds very promising for building a device. Quorum sensing may be very beneficial here.

Nicely worded intro sentence: “The noise sources in genetic circuits are most often found in pairs at the point of molecular synthesis (or polymerization or complex formation) and the associated point of decay due to random timing and discrete nature of these events.”

Zhou T, Chen L, Wang R, Aihara K. (2004). Intercellular communication induced by random fluctuations. Genome Informatics 15: 223 – 33.

Nice sentence: “In particular, gene regulation is an inherently noisy process, from transcriptional control, alternative splicing, translation, diffusion to chemical modification reactions of transcriptional factors, which all involve stochastic fluctuations owing to low copy numbers of man species per cell.”

This paper implements a multi-cell synthetic system model to show theoretically that noise can be exploited to facilitate mutual communication. Their model uses LuxI and LuxR with a pLacLux0 promoter. AI is distributed into the extracellular environment (Figure 1) and freely diffuses through cell membranes. I believe coupling here refers to synchronized behavior, but may just be the communication through AI signaling between two cells (sending to reception). Noise exists in the transcription and translation, AI synthesis, degradation reactions, diffusion, (and cell coupling).

Without noise, the system converges into a stable equilibrium. With strong noise, the multi-cell system is synchronously oscillated. This paper altogether supports that noise enhances temporal regularity of a dynamic system.

So this paper gives a lot of mathematical insight on noise enhancing an oscillatory system by quorum sensing. It is more in-depth than the Cox et al paper; it helps to identify the noisy factors that we can manipulate. Can speak w/ Dr. Heyer to understand it better.

Acar M, Becskei A, van Ourdenaarden A. (2005). Enhancement of cellular memory by reducing stochastic transitions. Nature 435: 228 – 32.

This paper was mentioned in the Kaern 2005 review. It explores the key parameters that determine the stability of cellular memory using the yeast galactose-signaling network as a model system. The system has three loops – 2 positive, 1 negative. Since there are 2 positive feedback loops, it’s possible to have multistability. They studied these feedback loops by doing loop knockouts. They put YFP under control of Gal1, so it’s expressed by the positive feedback loops (Figure 1). The positive mediated by Gal3p generates two stable expression states with persistent memory of previous galactose consumption states. The other positive loop amplifies the difference between the two states. The negative feedback loop reduces the strength of the first positive loop. (Figure 2) When they knocked out the negative feedback loop (Gal80), they found that the negative feedback loop weakens the effect of the positive feedback loop, and the system does not display a memory of the initial galactose consumption state. So the signaling pathway can store information on previous galactose exposures for generations. By opening the negative feedback loop, the memory persistence can be “tuned from hours to months”

By further understanding this system, we could use positive feedback loops (without a negative feedback loop) to differentiate cells into stable populations. But we can also introduce a similar negative feedback loop to allow switching between states.

Need to re-read this article more – don’t quite understand the memory component.

Stewart EJ, Madden R, Paul G, Taddei F. (2005). Aging and death in an organism that reproduces by morphologically symmetric division. PLoS Biol 3(2): e45.

This paper is looking for evidence of aging in E. coli as a challenge to (or support for) the theory that organisms with no distinction between the parent and offspring (asymmetric cell division and juvenile phase) do not age, therefore exhibiting functional immortality.

When E. coli divide, the rod shape of the two daughter cells have an old pole and a new pole. There is a slow turnover of cell wall components, so these stay for a relatively long time through generations. So they hypothesize that there may be a physiological asymmetry in the two poles instead of morphological asymmetry. By tracing the poles of the E. coli through the daughter cells, they found that the growth rate of the old pole cells is slower than that of the new pole cells, and the old pole cells do not produce as much daughter cell biomass as new pole cells. They called this age in bacteria.

I have very few ideas on how this paper would be useful for noise study. There is noise in the distribution of cellular components at the expense of old pole cells, so we could in some way use it to our advantage to have uneven distribution of cellular components for something, and the ones that randomly do not have enough of a certain component die. But in that case, it would have to be something critical to survival, or some sort of drug resistance, which is essentially what we already do with plasmids, and therefore not really a new application of noise.

Pin C, Rolfe MD, Muñoz-Cuevas M, Hinton JC, Peck MW, Walton NJ, Baranyi J. (2009). Network analysis of the transcriptional pattern of young and old cells of Escherichia coli during lag phase. BMC Syst Biol 16,3: 108.

This paper explores the transcriptional response of E. coli after conditional (starvation) senescence in 1 day (young) and 16 day (old) bacteria. Transcription analysis was performed with cells during the lag phase – after entering stationary senescence, and then being inoculated into new media, there is a lag phase before the next cell division.

In both old and young cells the number of genes down-regulated during lag was greater than those up-regulated. I didn’t get much out of this article. The conclusion “rejuvenation seems to take palce during exponential growth by replicative dilution of old cellular components” seems obvious particularly in light of the Stewart et al article tracking the old poles and new poles.

Jishage M, Kvint K, Shingler V, Nystrom T. (2002). Regulation of σ factor competition by the alarmone ppGpp. Genes Dev 16:1260 – 70.

Guanosine tetraphosphate, ppGpp, is an alarmone effector molecule that modulates control of ribosome production in E. coli. The nucleotide is produced by PSI and PSII synthetases encoded by relA and spoT. Binding of ppGpp to RNA polymerase stops rRNA biosynthesis as part of growth arrest, and induces some sigma 70-dependent genes (survival genes). Many operons encoding amino acid pathways require ppGpp – something to consider if messing with ppGpp. Sigma S transcription factor (mainenance and crossprotection genes) accumulates and directs RNA polymerase to genes used under conditions of starvation and stress. Sigma S requires ppGpp for its production. So ppGpp is required for multiple alternative sigma factors for induction.

The purpose of this paper was to examine how exactly ppGpp functions in affecting alternative sigma factors. They found that cells lacking ppGpp compete less effectively with the sigma 32 and sigma S binding versus sigma 70 binding of RNA polymerase. ppGpp is therefore the master regulator of sigmal factor transcription.

Orgel LE. (1963). The maintenance of the accuracy of protein synthesis and its relevance to ageing. Biochem 49: 517 – 21.

This paper was mentioned in Nystrom’s review on aging in bacteria. Orget presents a theory of aging / cell deterioration, error catastrophe. He begins by saying that although accumulation of DNA mutations has been discussed, there could be age-related consequences of transcription and translation errors due to faulty protein-synthesis apparatuses. Transcription errors in proteins involved in processing genetic information – determination of the sequences of nucleic acids and polypeptides – may lead to reduced specificity of the information-handling enzyme, and this leads to increasing error frequency. These processes are clearly cumulative and leads to error catastrophe. The initial error frequency corresponding to the amino acid substitution must be well-defined.

I was thinking perhaps you could switch amino acids in a directed place using Hin/hix. But using Orgel’s theory, that would require manipulating very key elements in the cell. Perhaps if instead you tied your synthetic system to something like Tet resistance gene so that if noise level of your system is too low, the cells can’t grow, and if too high, the Tet level becomes toxic. But then that would mean that the expression of your synthetic system would be dependent on the optimal Tet resistance level – which may not be what you want, and would not be tunable. Perhaps instead of Tet resistance you could tie your system reporter to a repressor for some promoter. The repressible promoter could express a restriction enzyme like ScaI that cuts AMP resistance. But then this would only ensure theoretically that the system works at a high enough level to produce enough repressor. It still wouldn’t be tunable, and “smart” cells could eventually mutate the repressible promoter so that the enzyme can never be expressed. Actually, maybe not, since once it happens once, that cell is out of the running.

This article unfortunately wasn’t as helpful as I had hoped. It’s rather cryptic, but there is more to be gotten out of it. The rest of the article talked about potential selection pressures particularly in higher organisms.

Qi B, Chi YM, Lo HK, Qian L. (2010). High-speed quantum random number generation by measuring phase noise of a single-mode laser. Optics Letters 35: 312 – 14.

This is a short physics paper that I skimmed in order to look into the thought process that goes into making a random number generator. “Random numbers have been widely used in many branches of science and technology, such as statistical analysis, computer simulation, and cryptography... true random numbers can be generated from fundamental quantum processes.” This one happens to be based on spontaneous emission, or phase noise, of a laser. The graph plotting the phase noise does resemble noise patterns measuring protein abundance in biological papers. It’s unclear how they got the random numbers generated by this system, but it was at least encouraging to find a source stating that the inherent stochastic behaviour of a system can generate true random numbers.

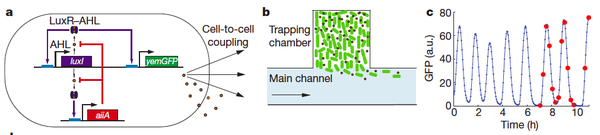
Danino T, Mondragon-palomino O, Tsimring L, Hasty J. (2010). A synchronized quorum of genetic clocks. Nature 463: 326 – 30.

This is another paper that utilizes the lux operon in order to achieve synchronization. The authors note that most quorum sensing systems require a critical cell density for generation of coordinated behaviour. They achieved this state by making a microfluidic device to control the concentration of cells and autoinducer. Figure 1 shows the construct design and the device. LuxI produces AHL – its own catalyzer and signal to other cells, and it also induces the production of AiiA which degrades AHL (LuxI also degrades quickly) – this sustains the oscillation. The period of oscillations is roughly proportional to the enzymatic protein decay time.

This paper was fine, but nothing particularly enlightening. This and most other oscillation papers I have found (and not summarized here) construct an oscillatory system solely to recreate a circadian rhythm. This paper did not provide any discussion of actual synthetic applications of an oscillatory system, other than to better understand the system in organisms.